1. Pengertian Transformasi Transformasi T dibidang adalah suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama.
Jenis-jenis transformasi yang dapat dilakukan antara lain :
- Translasi (Pergeseran)
- Refleksi (Pencerminan)
- Rotasi (Perputaran)
- Dilatasi (Perkalian)
2. Translasi dan Operasinya
Translasi (pergeseran) adalah pemindahan suatu objek sepanjang garis lurus dengan arah dan jarak tertentu.
Jika translasi
 memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
Contoh : Tentukan koordinat bayangan titik A (-3, 4) oleh translasi

Jawab :
Jawab :
A’ = ( -3 + 3, 4 + 6)
A’ = (0, 10)
3. Refleksi (Pencerminan)
a. Pencerminan terhadap sumbu x
Matriks percerminan :
b. Pencerminan Terhadap sumbu y
Matriks Pencerminan:
c. Pencerminan terhadap garis y = x
d. Pencerminan terhadap garis y = -x
Matriks Pencerminan:
e. Pencerminan terhadap garis x = h
Sehingga:
f. Pencerminan terhadap garis y=k
Sehingga:
g. Pencerminan terhadap titik asal O (0, 0)
Sehingga:
h. Pencerminan terhadap garis y = mx dimana m = tan q
Contoh :
Jawab :
Ambil sembarang titik pada garis y = 2x – 5, misalnya (x, y) dan titik bayangan oleh translasi  adalah (x’, y’) sehingga ditulis
adalah (x’, y’) sehingga ditulis 
 adalah (x’, y’) sehingga ditulis
adalah (x’, y’) sehingga ditulis 
Atau
Persamaan (1) dan (2) disubtitusikan pada persamaan garis semula, sehingga :
y = 2x – 5
y’ + 2 = 2 (x’- 3) – 5
y’ = 2x’ – 6 – 5 – 2
y’ = 2x’ – 13













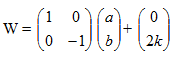






Tidak ada komentar:
Posting Komentar