Persamaan Lingkaran Garis Singgung
A. Persamaan Lingkaran yang berpusat di O (0, 0) dan berjari-jari r.

Dari gambar, diperoleh persamaan :
Sehingga diperoleh persamaan lingkaran dengan pusat di O dan berjari-jari r , yaitu :
Suatu titik A
 dikatakan :
dikatakan :a. Terletak pada lingkaran


b. Terletak di dalam lingkaran

c. Terletak di luar lingkaran

B. Persamaan Lingkaran yang berpusat di P (a, b) dan berjari-jari r.
Gambar di atas adalah sebuah lingkaran dengan pusat (a, b) dan berjari-jari r. Titik Q (x, y) adalah sebuah titik pada lingkaran.
Dari gambar diperoleh persamaan :
Suatu titik A
 dikatakan :
dikatakan :a. Terletak pada lingkaran

b. Terletak di dalam lingkaran

c. Terletak di luar lingkaran

C. Persamaan Umum Lingkaran
Bila kita menjabarkan persamaan :

Dan mengatur kembali suku-sukunya, maka akan diperoleh :
Persamaan terakhir dapat pula dinyatakan dengan :

Persamaan terakhir dapat pula dinyatakan dengan :

Dengan :


Persamaan (3) merupakan persamaan lingkaran dengan pusat di dan berjari-jari
dan berjari-jari 
D. Persamaan garis singgung lingkaran
1. Garis singgung lingkaran melalui sebuah titik lingkaran
* ditentukan dengan rumus
ditentukan dengan rumus 
* Persamaan garis singgung melaui titik P pada lingkaran
pada lingkaran
dinyatakan dengan rumus :

Maka persamaan garis singgungnya :
3. Garis singgung melalui sebuah titik diluar lingkaran Dari suatu titik P yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.
yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.
 terletak di luar garis lingkaran adalah :
terletak di luar garis lingkaran adalah : 
Langkah menentukan gradien ( m ) untuk persamaan (10) adalah sebagai berikut :
1. Substitusikan persamaan ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.
ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.
2. Dengan mengambil nilai D=0 , maka dipetoleh nilai m.


Persamaan (3) merupakan persamaan lingkaran dengan pusat di
 dan berjari-jari
dan berjari-jari 
D. Persamaan garis singgung lingkaran
1. Garis singgung lingkaran melalui sebuah titik lingkaran
*
 ditentukan dengan rumus
ditentukan dengan rumus 
* Persamaan garis singgung melaui titik P
 pada lingkaran
pada lingkaran
dinyatakan dengan rumus :

*Persamaan garis singgung melaui titik P pada lingkaran
pada lingkaran  dinyatakan dengan rumus :
dinyatakan dengan rumus : 
2. Garis singgung dengan gradien yang diketahui.
* Jika garis y = mx + n menyinggung lingkaran  pada lingkaran
pada lingkaran  dinyatakan dengan rumus :
dinyatakan dengan rumus : 
2. Garis singgung dengan gradien yang diketahui.

Maka persamaan garis singgungnya :

3. Garis singgung melalui sebuah titik diluar lingkaran Dari suatu titik P
 yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.
yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.  terletak di luar garis lingkaran adalah :
terletak di luar garis lingkaran adalah : 
Langkah menentukan gradien ( m ) untuk persamaan (10) adalah sebagai berikut :
1. Substitusikan persamaan
 ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.
ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.2. Dengan mengambil nilai D=0 , maka dipetoleh nilai m.

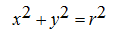



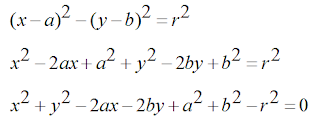

Tidak ada komentar:
Posting Komentar